1 X 2 2x 1
marihuanalabs
Sep 17, 2025 · 6 min read
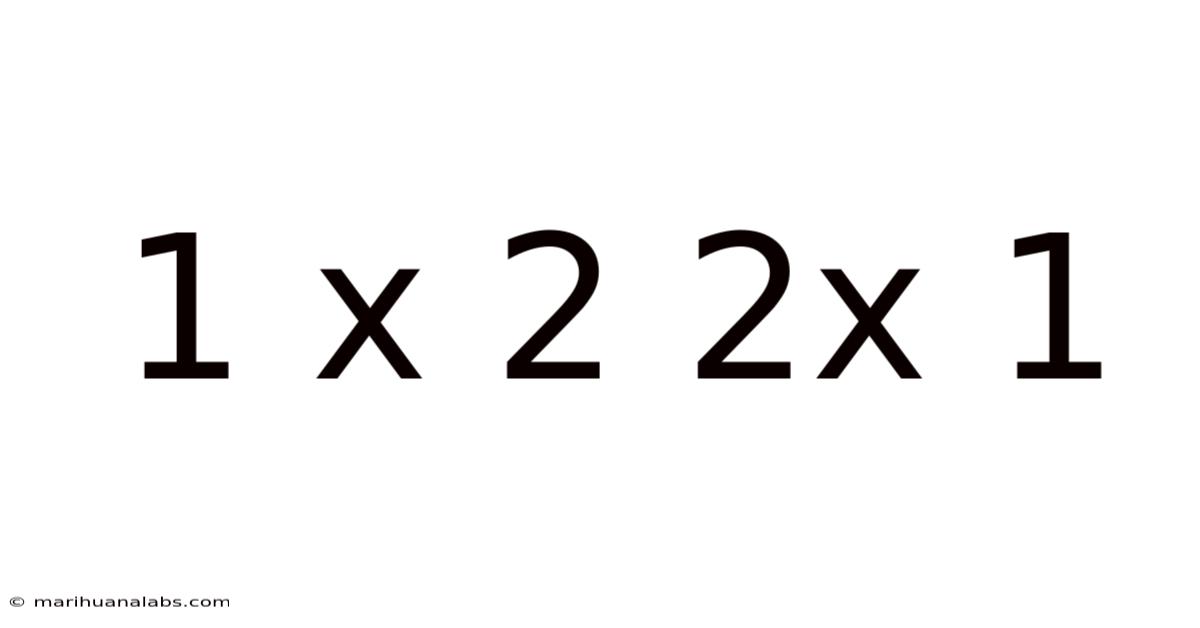
Table of Contents
Decoding the Enigma: A Deep Dive into the Mathematical Mystery of 1 x 2, 2 x 1, and Beyond
This article delves into the seemingly simple yet surprisingly rich mathematical concept surrounding the equations 1 x 2 and 2 x 1. While the answer – 2 – is immediately obvious to most, understanding the underlying principles reveals a gateway to more complex mathematical ideas, including the commutative property, the nature of multiplication, and its applications in various fields. We will explore these concepts in detail, moving beyond the basic answer to uncover the deeper meaning and significance of these simple expressions.
Understanding Multiplication: More Than Just Repeated Addition
At its core, multiplication is a shortcut for repeated addition. When we say 1 x 2, we are essentially asking, "What is the result of adding 1 to itself 2 times?" The answer, of course, is 1 + 1 = 2. Similarly, 2 x 1 asks, "What is the result of adding 2 to itself 1 time?" The answer remains 2. This seemingly simple explanation lays the foundation for a deeper understanding of the operations involved.
This fundamental understanding is crucial, especially when working with larger numbers or when introducing the concept to younger learners. Visual aids, such as using objects to represent the numbers and physically grouping them, can significantly enhance comprehension and make the process more intuitive. For example, imagine two groups of one apple each. This visually represents 2 x 1 = 2. Conversely, one group containing two apples clearly illustrates 1 x 2 = 2.
The Commutative Property: The Key to Understanding 1 x 2 and 2 x 1
The fact that both 1 x 2 and 2 x 1 equal 2 highlights a fundamental property of multiplication: the commutative property. This property states that the order of the numbers in a multiplication operation does not affect the result. In other words, a x b = b x a. This holds true for all real numbers. The commutative property is not just a mathematical quirk; it’s a fundamental principle that simplifies calculations and allows for flexibility in problem-solving.
Understanding the commutative property is essential for developing a robust understanding of algebra and higher-level mathematics. It allows us to manipulate equations more easily and to see relationships between seemingly different expressions. It’s a foundational concept that builds the groundwork for more complex mathematical operations and problem-solving.
Beyond the Basics: Exploring Applications in Different Fields
While 1 x 2 and 2 x 1 might seem trivial, their underlying principles have far-reaching applications across various fields. Let's explore some examples:
-
Computer Science: In programming, the commutative property is often exploited for optimization. The order of operations in certain calculations might not affect the final output, allowing programmers to choose the most efficient sequence.
-
Physics: Many physical laws and formulas rely on multiplication and the commutative property. For example, calculating work (Force x Distance) doesn’t change if we switch the order of force and distance.
-
Engineering: Engineering calculations often involve numerous multiplications, and understanding the commutative property helps in simplifying and verifying calculations.
-
Everyday Life: We use multiplication intuitively in daily life without explicitly thinking about it. Calculating the total cost of multiple items, determining the area of a room, or figuring out the number of items in a grid are all examples of everyday applications of multiplication.
Expanding the Concept: Multiplication with Larger Numbers
While the focus has been on 1 x 2 and 2 x 1, the commutative property extends to multiplication involving larger numbers. For example:
- 3 x 4 = 12 and 4 x 3 = 12
- 5 x 7 = 35 and 7 x 5 = 35
- 10 x 25 = 250 and 25 x 10 = 250
This consistency reinforces the universality of the commutative property in multiplication. It's a fundamental truth that underpins many complex mathematical operations.
Visualizing Multiplication: Area Models and Arrays
Visual representations can greatly enhance understanding, particularly for those who are new to the concepts of multiplication. Two powerful visualization tools include:
-
Area Models: Imagine a rectangle with a length of 2 units and a width of 1 unit. The area of this rectangle (length x width) represents 2 x 1 = 2 square units. Similarly, a rectangle with a length of 1 unit and a width of 2 units visually represents 1 x 2 = 2 square units.
-
Arrays: An array is a rectangular arrangement of objects. For example, an array of 2 rows and 1 column (2 x 1) contains 2 objects. Similarly, an array of 1 row and 2 columns (1 x 2) also contains 2 objects. These visual aids provide a concrete understanding of the relationship between multiplication and spatial representation.
Bridging the Gap: Connecting Multiplication to Other Mathematical Operations
Understanding multiplication allows for a deeper appreciation of its connection to other mathematical operations, such as:
-
Division: Multiplication and division are inverse operations. If 2 x 1 = 2, then 2 / 1 = 2 and 2 / 2 = 1.
-
Addition and Subtraction: While distinct, multiplication can be thought of as a more efficient way to perform repeated addition, and division as repeated subtraction.
-
Exponents: Multiplication forms the basis of exponents (repeated multiplication). For instance, 2² (2 squared) is equivalent to 2 x 2 = 4.
Addressing Common Misconceptions
Despite its apparent simplicity, some misconceptions can arise around multiplication:
-
Confusion with Addition: Some learners might initially confuse multiplication with addition. Emphasizing the repeated addition aspect of multiplication can help clarify this distinction.
-
Order of Operations: While the commutative property applies to multiplication alone, it's crucial to remember the order of operations (PEMDAS/BODMAS) when dealing with more complex expressions involving multiple operations.
Frequently Asked Questions (FAQ)
Q: Is the commutative property applicable to all mathematical operations?
A: No, the commutative property does not apply to all mathematical operations. While it holds true for addition and multiplication, it does not apply to subtraction or division. For example, 2 - 1 ≠ 1 - 2 and 2 / 1 ≠ 1 / 2.
Q: What is the significance of the commutative property in advanced mathematics?
A: The commutative property plays a crucial role in abstract algebra and other advanced mathematical fields. It forms the foundation for many important theorems and proofs, streamlining complex calculations and enabling the exploration of more abstract mathematical concepts.
Q: How can I effectively teach the concept of 1 x 2 and 2 x 1 to young children?
A: Use hands-on activities and visual aids. Counting objects, using arrays, and drawing pictures can make the concept more engaging and easier to understand for young learners. Relate it to real-world examples they can easily comprehend.
Conclusion: The Enduring Power of Simple Equations
The seemingly simple equations 1 x 2 and 2 x 1 offer a window into a vast world of mathematical principles. Beyond the straightforward answer of 2, these expressions reveal the power of the commutative property, the versatility of multiplication, and its significance across various fields. A deep understanding of these fundamental concepts is crucial for developing a strong foundation in mathematics, empowering learners to approach more complex mathematical problems with confidence and clarity. By appreciating the richness inherent in even the simplest mathematical expressions, we unlock a deeper appreciation for the elegance and power of mathematics itself.
Latest Posts
Latest Posts
-
Recette Potage De Chou Fleur
Sep 17, 2025
-
Craft Sales Winnipeg This Weekend
Sep 17, 2025
-
How To Adjust Drum Brakes
Sep 17, 2025
-
Hair Half Blonde Half Brown
Sep 17, 2025
-
Chords Whiskey In The Jar
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 X 2 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.