3/8 Is Bigger Than 1/2
marihuanalabs
Sep 24, 2025 · 6 min read
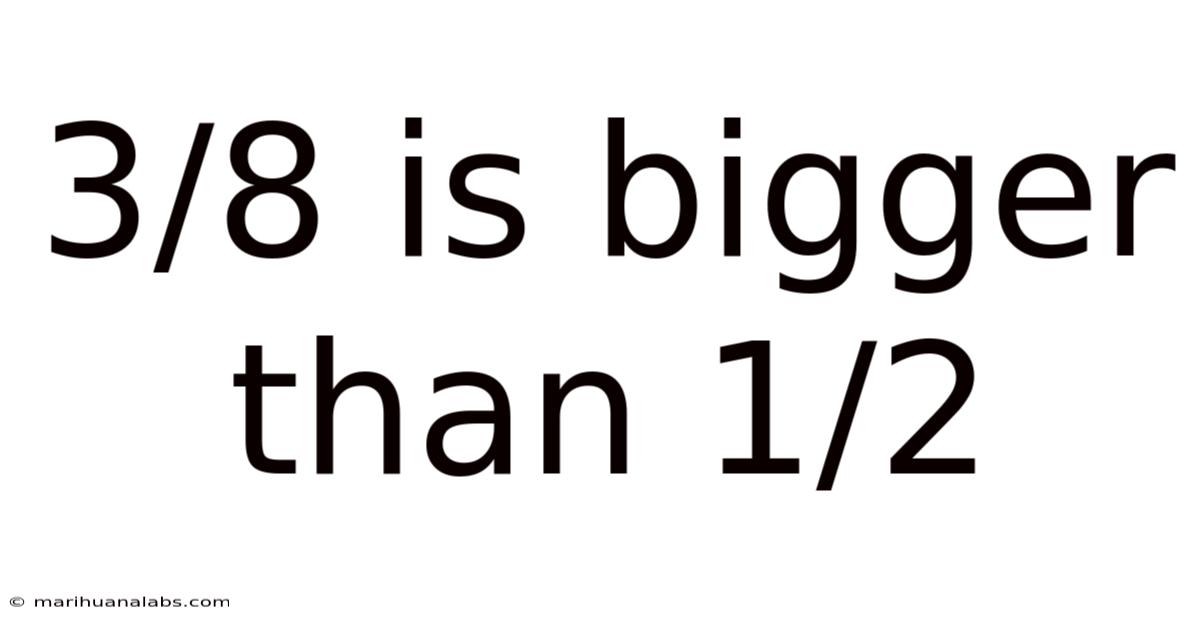
Table of Contents
Is 3/8 Bigger Than 1/2? Understanding Fractions and Comparisons
This article tackles a common misconception: the belief that 3/8 is larger than 1/2. We'll delve into the world of fractions, exploring how to compare them effectively, demystifying the process, and equipping you with the skills to confidently determine which fraction holds greater value. Understanding fraction comparison is crucial for various aspects of mathematics and everyday life, from baking to budgeting. This comprehensive guide will provide clear explanations, practical examples, and address frequently asked questions to ensure a thorough understanding of this fundamental mathematical concept.
Understanding Fractions: A Quick Refresher
Before we dive into comparing 3/8 and 1/2, let's ensure we have a solid grasp of what fractions represent. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we're considering.
For example, in the fraction 1/2, the denominator (2) tells us the whole is divided into two equal parts. The numerator (1) tells us we are considering one of those parts. Similarly, in 3/8, the whole is divided into eight equal parts, and we are considering three of them.
Comparing Fractions: Different Approaches
Several methods exist for comparing fractions. Let's explore the most common and effective approaches:
1. Finding a Common Denominator: This is arguably the most straightforward method. To compare fractions, we need to express them with the same denominator. This allows for a direct comparison of the numerators.
Let's compare 3/8 and 1/2 using this method:
-
Find the least common multiple (LCM) of the denominators: The denominators are 8 and 2. The LCM of 8 and 2 is 8.
-
Rewrite the fractions with the common denominator:
-
1/2 remains as is if we consider the denominator is already 8. To get to this, we multiplied the original denominator (2) by 4 to get 8. Thus we do the same for the numerator (1 x 4 = 4). Therefore 1/2 is equivalent to 4/8.
-
3/8 stays as it is.
-
-
Compare the numerators: Now we compare 3/8 and 4/8. Since 4 > 3, we conclude that 4/8 (or 1/2) is greater than 3/8.
2. Converting to Decimals: Another effective method involves converting the fractions into decimals. This allows for a direct numerical comparison.
-
Convert 3/8 to a decimal: Divide the numerator (3) by the denominator (8): 3 ÷ 8 = 0.375
-
Convert 1/2 to a decimal: Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
-
Compare the decimals: Since 0.5 > 0.375, we conclude that 1/2 is greater than 3/8.
3. Visual Representation: Visual aids can be incredibly helpful, especially when dealing with simpler fractions. Imagine a circle or a rectangle divided into equal parts. Shade the appropriate number of parts to represent each fraction. A visual comparison will clearly show which fraction represents a larger portion of the whole. For 3/8 and 1/2, the visual representation would show that 1/2 is significantly larger.
Why 3/8 is NOT Bigger Than 1/2: A Detailed Explanation
The statement "3/8 is bigger than 1/2" is incorrect. As demonstrated through the methods above, 1/2 is always greater than 3/8. Let's reiterate the key reasons:
-
Half is always greater than less than half: 1/2 represents exactly half of a whole. 3/8 represents less than half. To see this intuitively, consider dividing a pizza into 8 slices. 3 slices is less than half (4 slices) of the pizza.
-
Numerical Comparison: Regardless of the method used (common denominator, decimal conversion, or visual representation), the numerical comparison consistently demonstrates that 1/2 > 3/8.
-
Understanding the Magnitude: The denominator indicates the size of each part. A larger denominator means smaller parts. While 3/8 involves more parts (3) than 1/2 (1), those parts are significantly smaller. This is because the denominator 8 divides the whole into more pieces than the denominator 2.
Practical Applications and Real-World Examples
Understanding fraction comparison is essential in various real-world scenarios:
-
Cooking and Baking: Recipes often involve fractions. Accurately comparing fractions is crucial for measuring ingredients and ensuring the correct proportions.
-
Budgeting and Finance: Understanding fractions is essential when dealing with percentages, discounts, and calculating proportions of income and expenses.
-
Construction and Engineering: Precise measurements are critical, and fractions are frequently used to represent dimensions and proportions.
-
Data Analysis: Understanding fractions is crucial for interpreting data and percentages accurately in various fields.
-
Everyday tasks: Dividing tasks equally among group members, sharing items fairly, or simply understanding discounts at the store all necessitate understanding fractions.
Frequently Asked Questions (FAQ)
Q: Are there any shortcuts for comparing fractions?
A: While finding a common denominator is reliable, sometimes you can visually estimate. If the numerators are significantly smaller than their respective denominators (such as with 3/8 and 1/2), the fraction with the smaller denominator will usually be the bigger one.
Q: What if the denominators are large numbers?
A: For large denominators, using a calculator to convert to decimals can be faster and more efficient than finding a common denominator.
Q: How can I help my child understand fraction comparisons?
A: Use visual aids like pizza slices or blocks to represent fractions. Start with simple examples and gradually increase the complexity. Make it interactive and engaging, using games or real-life scenarios.
Q: Can I use cross-multiplication to compare fractions?
A: Yes, cross-multiplication is another valid method. To compare a/b and c/d, you cross-multiply: ad and bc. If ad > bc, then a/b > c/d. In our example: 32 = 6 and 81 = 8. Since 6 < 8, 3/8 < 1/2.
Conclusion
Understanding fraction comparison is a foundational skill in mathematics with broad real-world applications. While the statement "3/8 is bigger than 1/2" is incorrect, this article has provided several methods for accurately comparing fractions and highlighted the importance of this skill. By mastering these techniques, you can confidently navigate fraction comparisons in various contexts, from everyday life to complex mathematical problems. Remember to choose the method most comfortable and efficient for you, whether it be finding a common denominator, converting to decimals, using cross-multiplication, or employing visual representations. The key is to build a solid understanding of the underlying principles of fractions and their representation. This will empower you to approach and solve similar comparisons with ease and confidence.
Latest Posts
Latest Posts
-
Looking For Alaska Novel Summary
Sep 24, 2025
-
Poem Death Be Not Proud
Sep 24, 2025
-
Womens Swimsuits In The 1920s
Sep 24, 2025
-
Little Sister Dutch Indonesian Photos
Sep 24, 2025
-
Who Plays Martha May Whovier
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 3/8 Is Bigger Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.