Derivative Of X 2 2x
marihuanalabs
Sep 23, 2025 · 6 min read
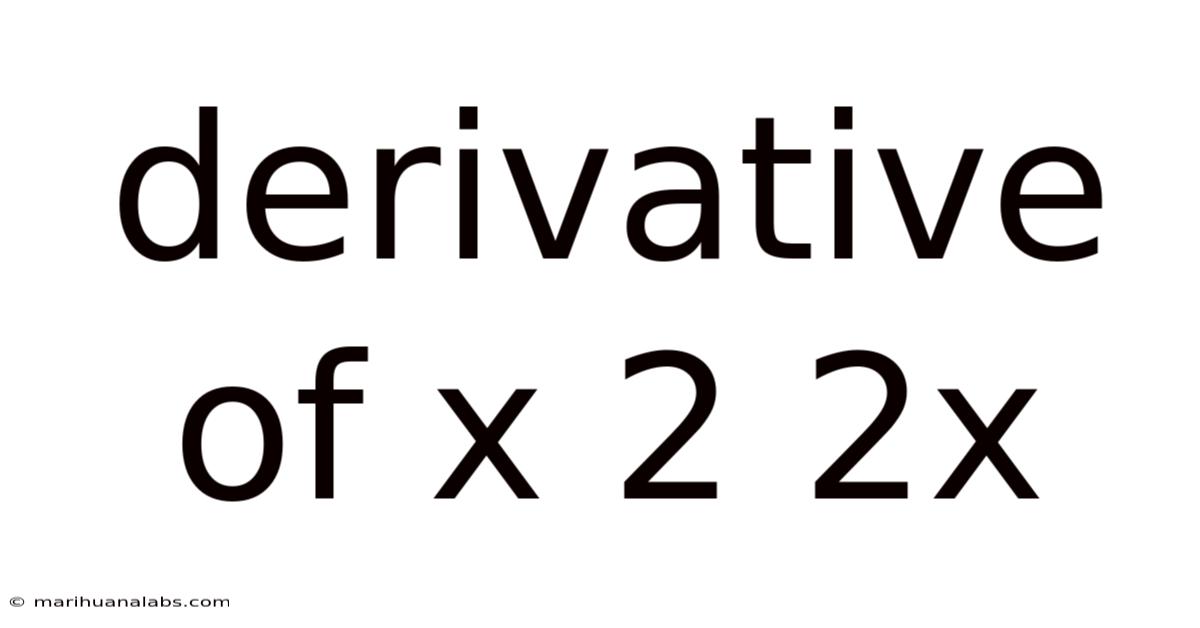
Table of Contents
Understanding the Derivative of x² + 2x: A Comprehensive Guide
Finding the derivative of a function is a fundamental concept in calculus. It allows us to understand the instantaneous rate of change of a function at any given point. This guide will walk you through calculating the derivative of the function f(x) = x² + 2x, explaining the underlying principles and providing a deeper understanding of the process. We'll explore different approaches, discuss the significance of the result, and address some frequently asked questions. This comprehensive guide is designed for students of all levels, from those just beginning their calculus journey to those looking to solidify their understanding of differentiation.
Introduction: What is a Derivative?
Before diving into the specifics of finding the derivative of x² + 2x, let's briefly review the concept of a derivative. The derivative of a function, often denoted as f'(x) or df/dx, represents the instantaneous rate of change of that function at a specific point. Geometrically, it represents the slope of the tangent line to the function's graph at that point. Intuitively, it tells us how much the function's output changes for a tiny change in its input.
The process of finding a derivative is called differentiation. Several methods exist, but we'll primarily focus on the power rule, a simple yet powerful technique for differentiating polynomial functions.
1. Applying the Power Rule to Find the Derivative
The power rule is a cornerstone of differentiation. It states that the derivative of xⁿ is nxⁿ⁻¹. Let's apply this rule to our function f(x) = x² + 2x.
Our function is a sum of two terms: x² and 2x. The derivative of a sum is simply the sum of the derivatives. Therefore, we can differentiate each term individually and then add the results.
-
Derivative of x²: Using the power rule with n = 2, the derivative of x² is 2x¹ = 2x.
-
Derivative of 2x: We can rewrite 2x as 2x¹, so applying the power rule with n = 1, the derivative is 2(1)x⁰ = 2 (remember that x⁰ = 1).
-
Combining the Derivatives: Since the derivative of a sum is the sum of the derivatives, the derivative of f(x) = x² + 2x is 2x + 2.
Therefore, f'(x) = 2x + 2. This means the instantaneous rate of change of the function x² + 2x at any point x is given by 2x + 2.
2. Understanding the Result: What does f'(x) = 2x + 2 mean?
The derivative, f'(x) = 2x + 2, provides valuable information about the original function f(x) = x² + 2x. Let's explore its significance:
-
Slope of the Tangent Line: At any point x on the graph of f(x), the slope of the tangent line is given by f'(x) = 2x + 2. This means the slope changes depending on the x-value.
-
Increasing and Decreasing Intervals: The derivative helps determine where the function is increasing or decreasing. If f'(x) > 0, the function is increasing; if f'(x) < 0, the function is decreasing. In our case, f'(x) = 2x + 2 > 0 when x > -1, indicating the function is increasing for x > -1. Conversely, f'(x) < 0 when x < -1, indicating the function is decreasing for x < -1.
-
Critical Points: Critical points occur where the derivative is zero or undefined. Setting f'(x) = 2x + 2 = 0, we find x = -1. This is a critical point, representing a potential minimum or maximum. Further analysis (using the second derivative test) would confirm that this is a minimum point.
3. Alternative Approaches to Differentiation
While the power rule is the most straightforward method for this specific function, let's briefly touch upon other approaches that could be used for more complex functions:
-
Limit Definition of the Derivative: This is the formal definition of the derivative:
f'(x) = lim (h→0) [(f(x + h) - f(x))/h]
While conceptually important, this method can be more cumbersome for complex functions. Applying it to f(x) = x² + 2x would involve substituting the function into the limit definition and simplifying the expression to arrive at 2x + 2.
-
Chain Rule: This rule is used for differentiating composite functions (functions within functions). While not necessary for this particular problem, understanding the chain rule is crucial for differentiating more advanced functions.
-
Product and Quotient Rules: These rules are used for differentiating products and quotients of functions, respectively. Again, they are not needed here, but are essential tools in a broader calculus context.
4. Graphical Representation and Interpretation
Visualizing the function and its derivative graphically reinforces understanding. The graph of f(x) = x² + 2x is a parabola that opens upwards. The vertex of this parabola is located at x = -1 (the critical point we found earlier). The graph of f'(x) = 2x + 2 is a straight line with a slope of 2 and a y-intercept of 2. The line intersects the x-axis at x = -1, confirming the critical point. The positive slope of the derivative for x > -1 shows the increasing nature of the original function in that region, and the negative slope for x < -1 indicates the decreasing nature.
5. Applications of Derivatives
Understanding derivatives has numerous applications across various fields:
-
Physics: Calculating velocity and acceleration (velocity is the derivative of position with respect to time, and acceleration is the derivative of velocity).
-
Economics: Determining marginal cost, marginal revenue, and marginal profit.
-
Engineering: Optimizing designs and processes.
-
Machine Learning: Gradient descent algorithms heavily rely on the concept of derivatives to find optimal solutions.
-
Computer Graphics: Derivatives are crucial for creating smooth curves and surfaces.
6. Frequently Asked Questions (FAQ)
-
Q: What if the function was more complex?
A: For more complex functions, you might need to use a combination of the power rule, chain rule, product rule, and quotient rule, depending on the function's structure.
-
Q: What is the significance of the second derivative?
A: The second derivative, f''(x), represents the rate of change of the first derivative. It indicates the concavity of the function (whether it's curving upwards or downwards). In our example, f''(x) = 2, which is always positive, indicating that the function f(x) is always concave up.
-
Q: Can the derivative be undefined?
A: Yes, the derivative can be undefined at points where the function is not differentiable (e.g., sharp corners or vertical tangents).
-
Q: What is the relationship between the derivative and the tangent line?
A: The derivative at a point gives the slope of the tangent line to the function's graph at that point.
-
Q: How can I apply this knowledge to real-world problems?
A: The applications are vast. For example, if f(x) represents the profit of a company as a function of the number of units produced, the derivative f'(x) represents the marginal profit—the additional profit gained from producing one more unit. Understanding this can help in making optimal production decisions.
Conclusion: Mastering the Fundamentals
Calculating the derivative of x² + 2x, while seemingly simple, lays the groundwork for understanding more complex differentiation problems. By mastering the power rule and understanding its implications, you build a strong foundation in calculus. Remember that the derivative provides crucial information about the behavior of a function, its rate of change, and its crucial points. The concepts explained here are fundamental tools for tackling more advanced problems in calculus and applying them to real-world scenarios. Continue practicing and exploring different functions to build your proficiency and confidence in this crucial area of mathematics.
Latest Posts
Latest Posts
-
Inventor H O W E
Sep 23, 2025
-
Words With The Prefix In
Sep 23, 2025
-
Hot Cross Buns Music Notes
Sep 23, 2025
-
Red Laced Blue Wyandotte Chicks
Sep 23, 2025
-
Sony Xperia Phones In Canada
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 2 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.