Derivative Of X 2 3
marihuanalabs
Sep 13, 2025 · 6 min read
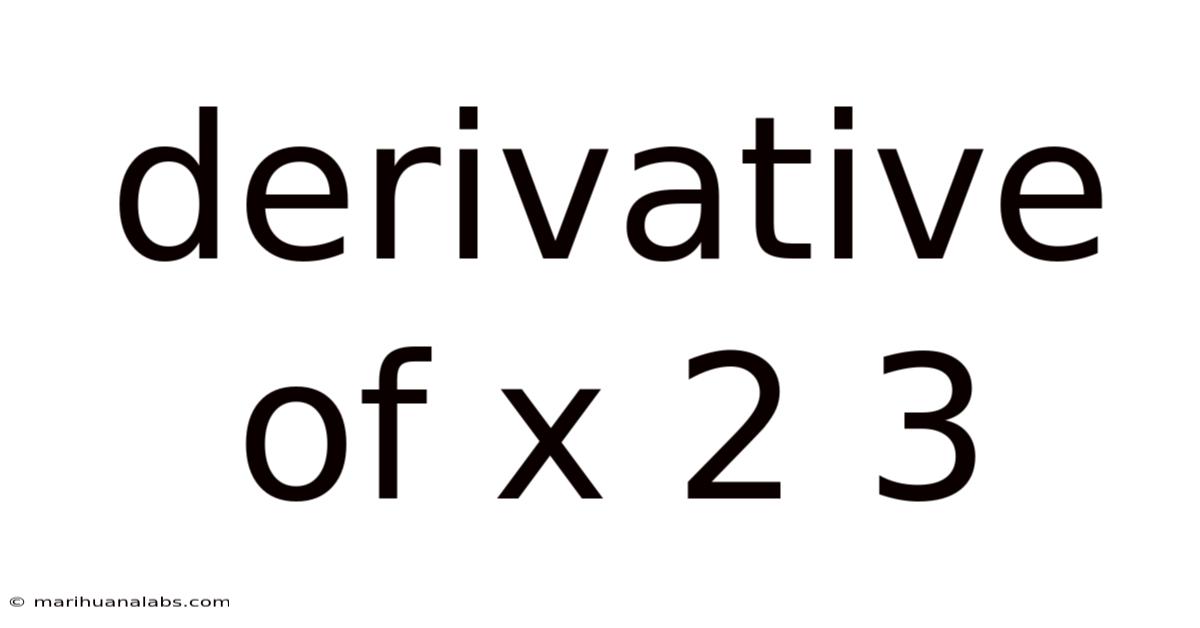
Table of Contents
Understanding the Derivative of x^(2/3): A Comprehensive Guide
Finding the derivative of x^(2/3) might seem daunting at first, especially if you're new to calculus. However, with a clear understanding of the power rule and a bit of practice, it becomes straightforward. This article will guide you through the process, explaining not only how to find the derivative but also the underlying principles and applications. We'll explore the power rule, delve into the mathematical reasoning behind it, and address common questions and misconceptions. By the end, you'll have a firm grasp of this important concept in calculus.
Introduction: What is a Derivative?
Before we tackle the derivative of x^(2/3), let's refresh our understanding of what a derivative actually represents. In simple terms, the derivative of a function at a specific point measures the instantaneous rate of change of that function at that point. Geometrically, it represents the slope of the tangent line to the function's graph at that point. This concept is fundamental in understanding how functions behave and is crucial in various fields like physics, engineering, and economics.
The derivative is a powerful tool for analyzing functions, allowing us to determine:
- Maximum and minimum values: By finding where the derivative is zero, we can locate potential maximum or minimum points on a function's graph.
- Increasing and decreasing intervals: The sign of the derivative tells us whether the function is increasing or decreasing over specific intervals.
- Concavity and inflection points: The second derivative (the derivative of the derivative) helps us determine the concavity of the function and locate inflection points, where the concavity changes.
- Optimization problems: Derivatives are essential for solving optimization problems, finding the best possible solution within given constraints.
The Power Rule: The Key to Finding Derivatives
The power rule is a fundamental theorem in differential calculus that simplifies the process of finding the derivative of power functions—functions of the form f(x) = xⁿ, where 'n' is a constant. The rule states:
If f(x) = xⁿ, then f'(x) = nxⁿ⁻¹
This rule applies to both positive and negative integer exponents, as well as rational and even irrational exponents. It's the cornerstone for calculating many derivatives, including the derivative of x^(2/3).
Deriving the Derivative of x^(2/3) using the Power Rule
Now, let's apply the power rule to find the derivative of our target function, f(x) = x^(2/3). According to the power rule:
-
Identify 'n': In our function, f(x) = x^(2/3), the exponent 'n' is 2/3.
-
Apply the power rule: We substitute 'n' into the power rule formula:
f'(x) = (2/3)x^((2/3) - 1)
-
Simplify the exponent:
(2/3) - 1 = (2/3) - (3/3) = -1/3
-
Write the final derivative:
Therefore, the derivative of x^(2/3) is:
f'(x) = (2/3)x^(-1/3)
This can also be written as:
f'(x) = 2 / (3x^(1/3)) or f'(x) = 2 / (3∛x)
Mathematical Justification of the Power Rule (for the interested reader)
The power rule isn't just a magical formula; it's derived from the definition of the derivative using limits. While a full derivation is beyond the scope of a beginner's guide, we can outline the key steps:
The definition of the derivative is:
f'(x) = lim (h→0) [(f(x + h) - f(x)) / h]
For f(x) = xⁿ, this becomes:
f'(x) = lim (h→0) [((x + h)ⁿ - xⁿ) / h]
This limit requires manipulation using the binomial theorem, which expands (x + h)ⁿ into a sum of terms involving x and h. After simplification and cancellation, the limit evaluates to nxⁿ⁻¹, proving the power rule. This process involves algebraic manipulation and a strong understanding of limit properties, which are usually covered in detail in a calculus course.
Understanding the Derivative's Meaning in the Context of x^(2/3)
The derivative, f'(x) = (2/3)x^(-1/3), tells us the instantaneous rate of change of the function f(x) = x^(2/3) at any point x. Let's analyze this further:
-
x > 0: For positive values of x, the derivative is positive, indicating that the function f(x) = x^(2/3) is increasing. The rate of increase slows down as x increases.
-
x < 0: For negative values of x, the derivative is negative, meaning the function is decreasing. The rate of decrease also slows down as the absolute value of x increases.
-
x = 0: The derivative is undefined at x = 0. This is because the tangent line to the graph of f(x) = x^(2/3) at x = 0 is vertical, and a vertical line has an undefined slope. This point is a cusp in the graph.
The graph of y = x^(2/3) visually demonstrates these characteristics. It has a distinctive cusp at the origin (0,0), illustrating the undefined derivative at that point.
Applications of the Derivative of x^(2/3)
The derivative of x^(2/3) finds applications in various fields:
-
Optimization problems: In optimization problems where the objective function involves a term like x^(2/3), finding the derivative is crucial for determining critical points and identifying optimal solutions. This could be applicable in designing structures, optimizing production processes, or analyzing economic models.
-
Physics: In physics, especially in mechanics and dynamics, the derivative represents instantaneous rates of change, such as velocity (derivative of position) or acceleration (derivative of velocity). Functions involving fractional exponents can describe certain types of motion or forces.
-
Economics: Economic models often use fractional exponents to represent phenomena like returns to scale or utility functions. Calculating the derivative helps analyze marginal changes and optimize economic outcomes.
Frequently Asked Questions (FAQ)
Q: Can I use the power rule for any exponent?
A: Yes, the power rule applies to a wide range of exponents, including rational (fractions), irrational (like π or √2), and negative numbers.
Q: What if the function is more complex than just x^(2/3)?
A: If the function involves other terms or operations (addition, multiplication, etc.), you'll need to apply other differentiation rules like the sum rule, product rule, or chain rule in combination with the power rule.
Q: What does x^(-1/3) mean?
A: x^(-1/3) is equivalent to 1/∛x or 1/(x^(1/3)). A negative exponent indicates the reciprocal of the base raised to the positive exponent.
Q: How can I graph y = x^(2/3)?
A: You can use graphing software or a graphing calculator to visualize the graph. Observe the cusp at the origin and the increasing nature of the function for positive x values.
Q: Is the derivative always defined?
A: No. The derivative might be undefined at certain points, such as cusps or points of discontinuity. The derivative of x^(2/3) is undefined at x=0.
Conclusion
Finding the derivative of x^(2/3) may initially appear challenging but is quite manageable using the fundamental power rule of calculus. Understanding this seemingly simple derivative unlocks deeper insights into calculus and its applications in diverse fields. Remember that the derivative provides crucial information about the rate of change of a function, enabling us to analyze its behavior and solve optimization problems. This comprehensive guide provided a thorough understanding of the derivative, its derivation, significance, and applications, empowering you to tackle similar problems with confidence. By grasping these concepts, you'll build a strong foundation for your continued journey in calculus.
Latest Posts
Latest Posts
-
Canuckle Word Game Online Canadian
Sep 13, 2025
-
Bend It Like Beckham Ost
Sep 13, 2025
-
Assisted Living Prince Albert Sk
Sep 13, 2025
-
Representing Numbers In Different Ways
Sep 13, 2025
-
The Fox Le Petit Prince
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.