Is 3/16 Smaller Than 1/4
marihuanalabs
Sep 15, 2025 · 6 min read
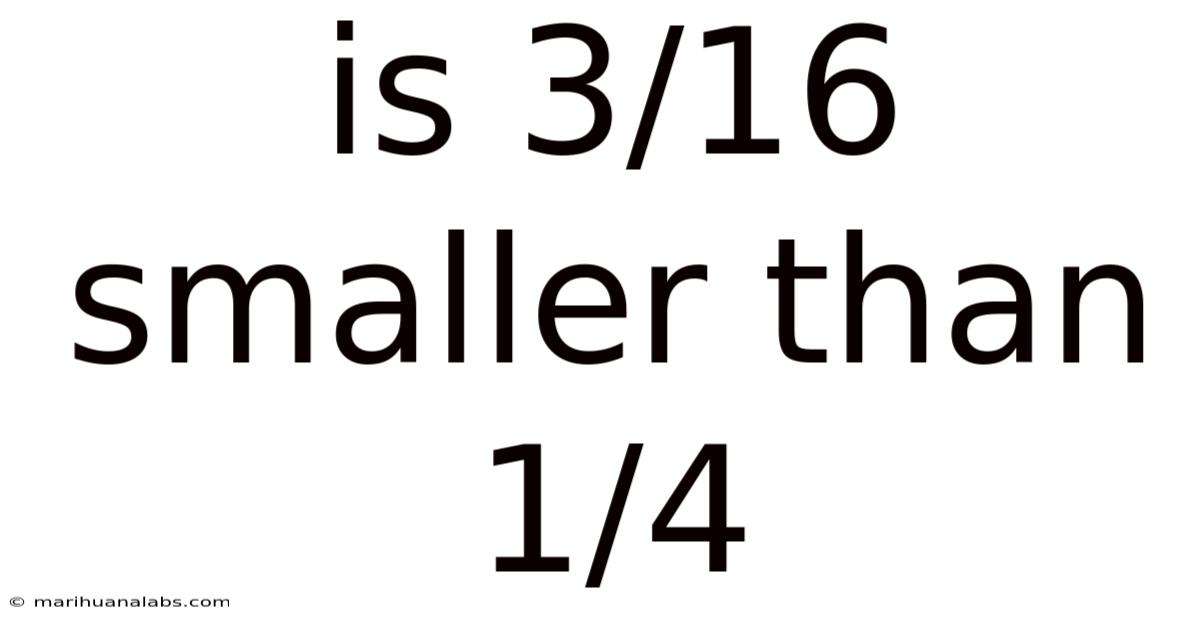
Table of Contents
Is 3/16 Smaller Than 1/4? A Deep Dive into Fraction Comparison
This article explores the question: is 3/16 smaller than 1/4? We'll delve into the methods for comparing fractions, providing a clear and comprehensive understanding, not just of this specific comparison, but also of the broader concept of fraction manipulation. Understanding fraction comparison is a fundamental skill in mathematics with applications across various fields, from cooking and construction to advanced scientific calculations.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the whole is divided into 4 equal parts, and we're considering 3 of those parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can directly compare their numerators. The fraction with the larger numerator is the larger fraction.
Let's apply this method to compare 3/16 and 1/4:
-
Find the least common multiple (LCM) of the denominators: The denominators are 16 and 4. The multiples of 4 are 4, 8, 12, 16, 20... and the multiples of 16 are 16, 32, 48... The least common multiple is 16.
-
Convert the fractions to have the common denominator:
- 3/16 already has a denominator of 16, so it remains as 3/16.
- To convert 1/4 to have a denominator of 16, we multiply both the numerator and the denominator by 4: (1 x 4) / (4 x 4) = 4/16.
-
Compare the numerators: Now we compare 3/16 and 4/16. Since 3 < 4, we conclude that 3/16 < 4/16.
-
Conclusion: Therefore, 3/16 is smaller than 1/4.
Method 2: Converting to Decimals
Another effective method is to convert both fractions to decimals. This involves dividing the numerator by the denominator for each fraction. Then, we can compare the resulting decimal values.
-
Convert 3/16 to a decimal: 3 ÷ 16 = 0.1875
-
Convert 1/4 to a decimal: 1 ÷ 4 = 0.25
-
Compare the decimals: Since 0.1875 < 0.25, we conclude that 3/16 < 1/4.
-
Conclusion: Again, we find that 3/16 is smaller than 1/4.
Method 3: Visual Representation
While not as precise as the previous methods for complex fractions, visualizing fractions can be helpful for understanding the comparison, especially for simpler fractions. Imagine two identical pizzas.
-
1/4: One pizza is cut into four equal slices. 1/4 represents one of these slices.
-
3/16: The other pizza is cut into sixteen equal slices. 3/16 represents three of these slices.
Visually, it's easy to see that three slices out of sixteen are smaller in total area than one slice out of four. This confirms that 3/16 is smaller than 1/4.
A Deeper Dive into Fraction Comparison Techniques
The methods described above are foundational, but mastering fraction comparison requires a more nuanced understanding. Let's explore some advanced considerations:
-
Improper Fractions: Improper fractions have a numerator larger than or equal to the denominator (e.g., 5/4). When comparing improper fractions, the same methods apply – find a common denominator or convert to decimals. However, remember that an improper fraction is always greater than or equal to 1.
-
Mixed Numbers: Mixed numbers combine a whole number and a fraction (e.g., 1 3/4). To compare mixed numbers, you can either convert them to improper fractions and then use the previously described methods, or compare the whole number parts first, and if they are equal, compare the fractional parts.
-
Equivalent Fractions: It's crucial to understand equivalent fractions. These are fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 = 2/4 = 4/8). Simplifying fractions to their lowest terms (by dividing both the numerator and denominator by their greatest common divisor) can aid in comparison. For example, comparing 6/8 and 3/4 is easier if you simplify 6/8 to 3/4, revealing they are equivalent.
-
Cross-Multiplication: For comparing two fractions, a shortcut is cross-multiplication. Multiply the numerator of the first fraction by the denominator of the second, and vice versa. The larger product corresponds to the larger fraction. For example, comparing 3/16 and 1/4: (3 x 4) = 12 and (16 x 1) = 16. Since 12 < 16, 3/16 < 1/4.
Practical Applications of Fraction Comparison
The ability to compare fractions is not just an academic exercise; it has significant practical applications:
-
Cooking and Baking: Recipes often require precise measurements, and understanding fractions is crucial for adjusting ingredient quantities.
-
Construction and Engineering: Accurate measurements are essential in construction and engineering projects, and fraction comparison helps ensure the correct proportions and dimensions.
-
Finance: Calculating percentages, interest rates, and proportions of investments all involve fractions.
-
Data Analysis: Interpreting data often requires comparing fractions and proportions.
Frequently Asked Questions (FAQ)
Q: Are there any online tools or calculators to help compare fractions?
A: Yes, many online calculators and websites are available to assist with fraction comparison. These tools can be particularly helpful for more complex fractions.
Q: Why is finding a common denominator the most reliable method?
A: Finding a common denominator ensures that you are comparing like quantities. By expressing both fractions with the same denominator, you directly compare the numerators, which represent the number of parts of the same size.
Q: What if I get a fraction that is not in its simplest form?
A: It's always best practice to simplify fractions to their lowest terms before comparing them. This makes the comparison easier and less prone to errors. Simplifying involves dividing both the numerator and denominator by their greatest common divisor.
Q: Is there a fastest way to compare fractions?
A: The fastest method depends on the specific fractions involved. For simple fractions, visual comparison or a quick decimal conversion might be quickest. For more complex fractions, the common denominator or cross-multiplication methods are generally more efficient.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through numerous examples, using different comparison methods to build your confidence and understanding. Try to visualize the fractions, and use real-world scenarios to reinforce your learning.
Conclusion
We've conclusively demonstrated that 3/16 is smaller than 1/4 using multiple methods. Mastering fraction comparison is a crucial skill in mathematics with broad real-world applications. By understanding the various methods – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – you can confidently approach fraction comparisons of any complexity. Remember that consistent practice and a solid grasp of fundamental fraction concepts are key to success. Don't hesitate to use visual aids and real-world examples to reinforce your learning and build your mathematical confidence.
Latest Posts
Latest Posts
-
Pouding Bleuets Recette De Maman
Sep 15, 2025
-
The Land Of Stories Order
Sep 15, 2025
-
Labrador Breeders In Bc Canada
Sep 15, 2025
-
Passe Compose Etre And Avoir
Sep 15, 2025
-
Make A Plan Stan Lyrics
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is 3/16 Smaller Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.