Is 3/4 Bigger Than 1/3
marihuanalabs
Sep 18, 2025 · 5 min read
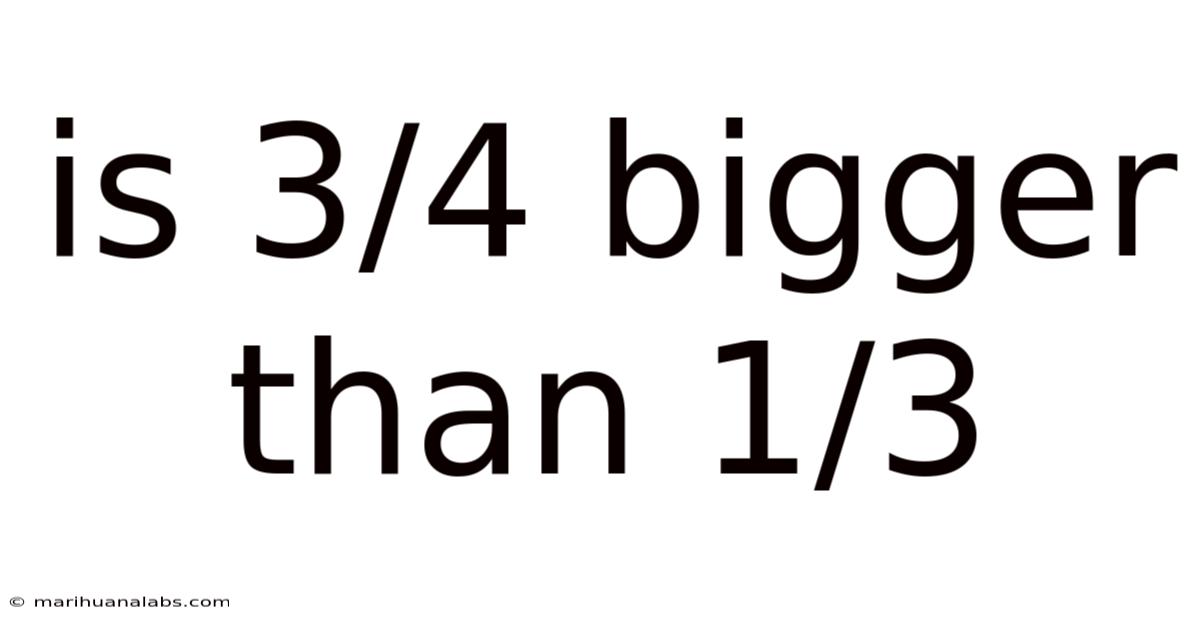
Table of Contents
Is 3/4 Bigger Than 1/3? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will comprehensively explore the question, "Is 3/4 bigger than 1/3?", providing not just the answer but a thorough understanding of fraction comparison techniques. We'll delve into various methods, explain the underlying mathematical principles, and address common misconceptions. By the end, you'll be equipped with the confidence to compare any two fractions accurately and efficiently.
Introduction: Understanding Fractions
Before jumping into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts we're considering. For example, in the fraction 3/4, the whole is divided into 4 equal parts, and we're considering 3 of those parts.
Method 1: Visual Comparison
One of the easiest ways to compare fractions, especially for beginners, is through visual representation. Imagine two identical pies.
- Pie 1: Cut into 4 equal slices. Take 3 slices (representing 3/4).
- Pie 2: Cut into 3 equal slices. Take 1 slice (representing 1/3).
Visually, it's clear that 3 slices from a pie cut into 4 is a larger portion than 1 slice from a pie cut into 3. Therefore, 3/4 is bigger than 1/3. This method provides an intuitive understanding but isn't practical for comparing more complex fractions.
Method 2: Finding a Common Denominator
A more robust and universally applicable method involves finding a common denominator. This means converting both fractions so they have the same denominator. The least common denominator (LCD) is the smallest number that both denominators divide into evenly.
Let's compare 3/4 and 1/3.
-
Find the LCD: The denominators are 4 and 3. The least common multiple of 4 and 3 is 12.
-
Convert the fractions:
- To convert 3/4 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12.
- To convert 1/3 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 4: (1 x 4) / (3 x 4) = 4/12.
-
Compare the numerators: Now that both fractions have the same denominator, we compare the numerators. 9/12 is greater than 4/12.
Therefore, 3/4 (which is equal to 9/12) is bigger than 1/3 (which is equal to 4/12).
Method 3: Converting to Decimals
Another effective method is to convert both fractions to decimals. This involves dividing the numerator by the denominator.
- 3/4 = 3 ÷ 4 = 0.75
- 1/3 = 1 ÷ 3 ≈ 0.333... (this is a recurring decimal)
Comparing the decimal values, 0.75 is clearly larger than 0.333... Thus, 3/4 is bigger than 1/3. This method is particularly useful when dealing with fractions that are difficult to visualize or find a common denominator for easily.
Method 4: Using Cross-Multiplication
Cross-multiplication provides a quick way to compare fractions. This method works by multiplying the numerator of one fraction by the denominator of the other, and vice-versa. Compare the resulting products.
-
Cross-multiply 3/4 and 1/3:
- 3 x 3 = 9
- 4 x 1 = 4
-
Compare the products: Since 9 > 4, 3/4 is greater than 1/3.
This method is efficient but might require a deeper understanding of the underlying mathematical principles to fully grasp why it works.
The Mathematical Rationale Behind Fraction Comparison
All the methods described above stem from the fundamental principle that fractions represent portions of a whole. When comparing fractions, we're essentially comparing the relative sizes of these portions. Finding a common denominator ensures we're comparing like-for-like, allowing for a direct comparison of the numerators. Converting to decimals provides a standardized numerical representation for easy comparison. Cross-multiplication is a shortcut that effectively achieves the same result as finding a common denominator.
Addressing Common Misconceptions
A common misconception is that larger numerators always indicate a larger fraction. This is incorrect without considering the denominator. For example, 1/2 is greater than 1/10, even though 10 is larger than 2. The size of the denominator significantly impacts the overall size of the fraction.
Another misconception arises when comparing fractions with different denominators without finding a common denominator or using another appropriate method. Simply comparing numerators or denominators in isolation leads to inaccurate conclusions.
Frequently Asked Questions (FAQ)
Q: Can I always use cross-multiplication to compare fractions?
A: Yes, cross-multiplication is a valid method for comparing two fractions. It's a shortcut that simplifies the process.
Q: Is there a fastest method for comparing fractions?
A: The "fastest" method depends on the specific fractions and your familiarity with different techniques. For simple fractions, visual comparison might be quickest. For more complex fractions, cross-multiplication or converting to decimals might be more efficient.
Q: What if I have more than two fractions to compare?
A: To compare more than two fractions, you can use any of the methods mentioned above, comparing them pairwise or finding a common denominator for all fractions and then comparing their numerators.
Q: Why is it important to learn about comparing fractions?
A: Comparing fractions is a crucial skill for various aspects of life, from baking and cooking to understanding financial data and solving mathematical problems. A strong grasp of fraction comparison enhances problem-solving abilities and builds a solid foundation for more advanced mathematical concepts.
Conclusion: Mastering Fraction Comparison
Determining whether 3/4 is bigger than 1/3 is a simple yet illustrative example of comparing fractions. This article has explored several effective methods – visual comparison, finding a common denominator, converting to decimals, and cross-multiplication – providing a comprehensive understanding of the underlying mathematical principles. By mastering these techniques, you can confidently compare any two fractions, ensuring accuracy and enhancing your mathematical proficiency. Remember, the key is to find a method you understand well and apply it consistently. With practice, comparing fractions will become second nature, empowering you to tackle more complex mathematical challenges with ease and confidence. The ability to accurately and quickly compare fractions is a valuable asset in numerous aspects of life, underlining the importance of mastering this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Parts Of Inside A Car
Sep 18, 2025
-
Cutting Aluminum With Plasma Cutter
Sep 18, 2025
-
Wh Auden The Unknown Citizen
Sep 18, 2025
-
Renew Philippine Passport In Philippines
Sep 18, 2025
-
Beauty Essex Restaurant New York
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Bigger Than 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.