Is 3/8 Smaller Than 3/4
marihuanalabs
Sep 24, 2025 · 5 min read
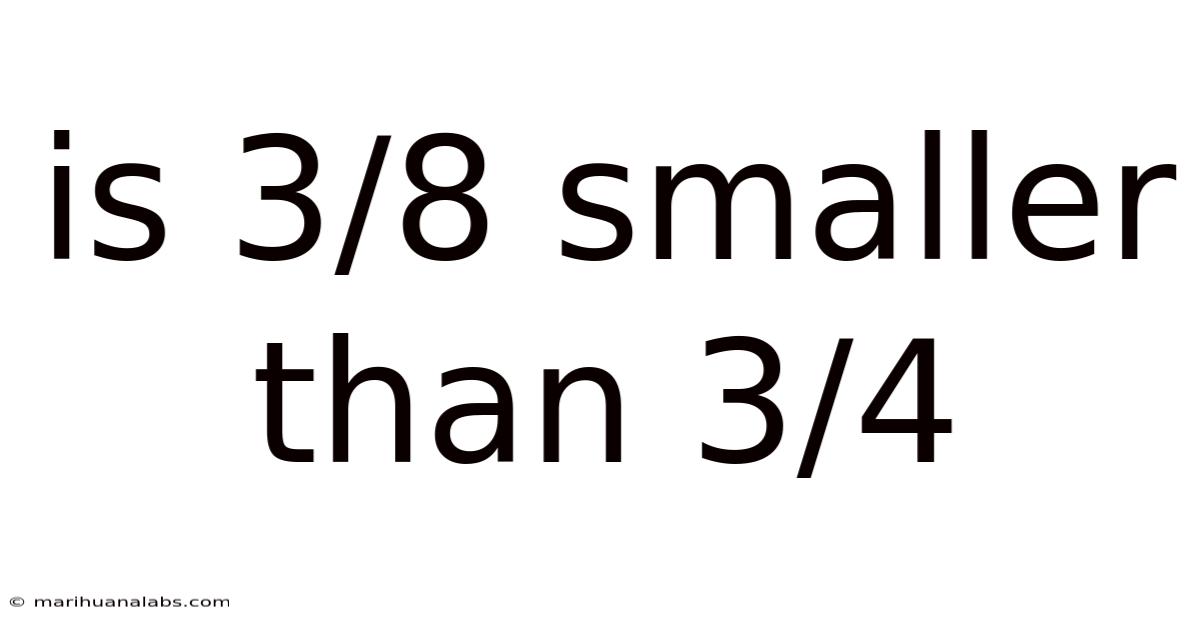
Table of Contents
Is 3/8 Smaller Than 3/4? A Deep Dive into Fraction Comparison
Understanding fractions is a cornerstone of mathematical literacy. This article will comprehensively explore the question, "Is 3/8 smaller than 3/4?", providing not just a simple yes or no answer, but a thorough explanation suitable for learners of all levels. We'll delve into various methods for comparing fractions, exploring the underlying principles and building a strong foundation for future fractional calculations. This will include visual representations, numerical comparisons, and a look at the underlying mathematical concepts. By the end, you'll not only know the answer but also understand why it's the answer.
Introduction: Understanding Fractions
Before we tackle the specific comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering.
For example, in the fraction 3/4, the denominator (4) indicates that the whole is divided into four equal parts. The numerator (3) tells us we are considering three of those four parts.
Visualizing the Comparison: Using Fraction Bars
A visual approach can be incredibly helpful when comparing fractions. Let's represent 3/8 and 3/4 using fraction bars:
Imagine two identical bars. Divide the first bar into 8 equal sections and shade in 3 of them. This represents 3/8. Now, divide the second bar into 4 equal sections and shade in 3 of them. This represents 3/4. By visually comparing the shaded areas, it's immediately clear that the shaded portion representing 3/4 is significantly larger than the shaded portion representing 3/8.
Numerical Comparison: Finding a Common Denominator
While visual aids are excellent for understanding, numerical comparison provides a more rigorous and generalizable method. To compare fractions directly, we need to find a common denominator. This is a number that is a multiple of both denominators.
In our case, we have 3/8 and 3/4. The denominators are 8 and 4. Multiples of 4 are 4, 8, 12, 16… and multiples of 8 are 8, 16, 24… The least common multiple (LCM) of 8 and 4 is 8.
Now, we convert both fractions to have a denominator of 8:
- 3/4 remains unchanged because it already has an equivalent fraction with 8 as the denominator. We can multiply both numerator and denominator of 3/4 by 2 to obtain 6/8.
- 3/8 remains as it is.
Now we have 3/8 and 6/8. Since both fractions share the same denominator, we can directly compare their numerators. Clearly, 3 is smaller than 6. Therefore, 3/8 is smaller than 6/8, which is equivalent to 3/4.
Decimal Conversion: Another Approach
Another way to compare fractions is to convert them into decimals. This method is particularly helpful when dealing with more complex fractions or when you need to perform further calculations. To convert a fraction to a decimal, we simply divide the numerator by the denominator:
- 3/8 = 0.375
- 3/4 = 0.75
Comparing the decimal values, 0.375 is clearly less than 0.75. This confirms that 3/8 is smaller than 3/4.
Understanding the Relationship Between Numerator and Denominator
The relationship between the numerator and the denominator significantly impacts the value of a fraction. A larger numerator relative to the denominator indicates a larger fraction. However, when comparing fractions with different denominators, the size of the denominator also plays a crucial role.
In our example, both fractions have the same numerator (3). However, 3/4 has a smaller denominator (4) than 3/8 (denominator of 8). A smaller denominator means each part of the whole is larger. Therefore, three parts of a whole divided into four (3/4) represent a larger portion than three parts of a whole divided into eight (3/8).
Proportion and Ratio: A Deeper Look
The concept of proportion and ratio underpins our understanding of fractions. A ratio expresses the relative sizes of two or more values. In the context of our fractions, we can consider the ratio of the numerator to the denominator. For 3/4, the ratio is 3:4, while for 3/8, the ratio is 3:8. The smaller the ratio value, the smaller the fraction.
Cross-Multiplication Method for Comparing Fractions
Another powerful technique for comparing fractions is cross-multiplication. This method avoids the need to find a common denominator and works efficiently for comparing any two fractions.
To compare fractions a/b and c/d, we cross-multiply:
- Calculate a * d
- Calculate b * c
If a * d > b * c, then a/b > c/d. If a * d < b * c, then a/b < c/d. If a * d = b * c, then a/b = c/d.
Let's apply this to 3/8 and 3/4:
- 3 * 4 = 12
- 8 * 3 = 24
Since 12 < 24, we conclude that 3/8 < 3/4.
Frequently Asked Questions (FAQ)
Q: Are there any other ways to compare fractions?
A: Yes! You can use number lines, diagrams representing parts of a whole, or even convert the fractions to percentages.
Q: What if the fractions have different numerators and denominators?
A: Finding a common denominator or using cross-multiplication remains the most reliable methods.
Q: Why is understanding fractions important?
A: Fractions are fundamental to many areas, including measurement, cooking, construction, and advanced mathematics. A solid understanding of fractions is essential for success in various fields.
Q: How can I improve my skills in comparing fractions?
A: Practice is key! Work through various examples, use different methods, and check your answers. Use online resources and interactive tools to enhance your learning experience.
Conclusion: Mastering Fraction Comparison
In conclusion, 3/8 is definitively smaller than 3/4. We've explored multiple methods to demonstrate this, from visual representations using fraction bars to numerical comparisons involving common denominators, decimal conversions, and cross-multiplication. Understanding the relationship between the numerator and denominator, as well as the concepts of proportion and ratio, provides a deeper insight into fraction comparison. Mastering these techniques will empower you to confidently tackle more complex fraction problems and build a strong foundation in mathematics. Remember, the key to mastering fractions lies in consistent practice and exploring different approaches to problem-solving.
Latest Posts
Latest Posts
-
Silver Lab Puppies For Sale
Sep 24, 2025
-
Deciduous Trees And Coniferous Trees
Sep 24, 2025
-
Light Up The Night Almonte
Sep 24, 2025
-
Pain Aux Bananes Sans Oeufs
Sep 24, 2025
-
Best Nail Salon Windsor Ontario
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Is 3/8 Smaller Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.